1.1. 注意力机制

Attention? Attention!

简而言之，深度学习中的注意力可以被广义地解释为重要性权重向量：为了预测或推断一个元素，例如图像中的一个像素或句子中的一个单词，我们使用注意力向量来估计它与其他元素的相关性（或 "关注"，您可能在许多论文中读到过），并将它们的值之和经注意力向量加权后作为目标的近似值。

1.2. 为翻译而生

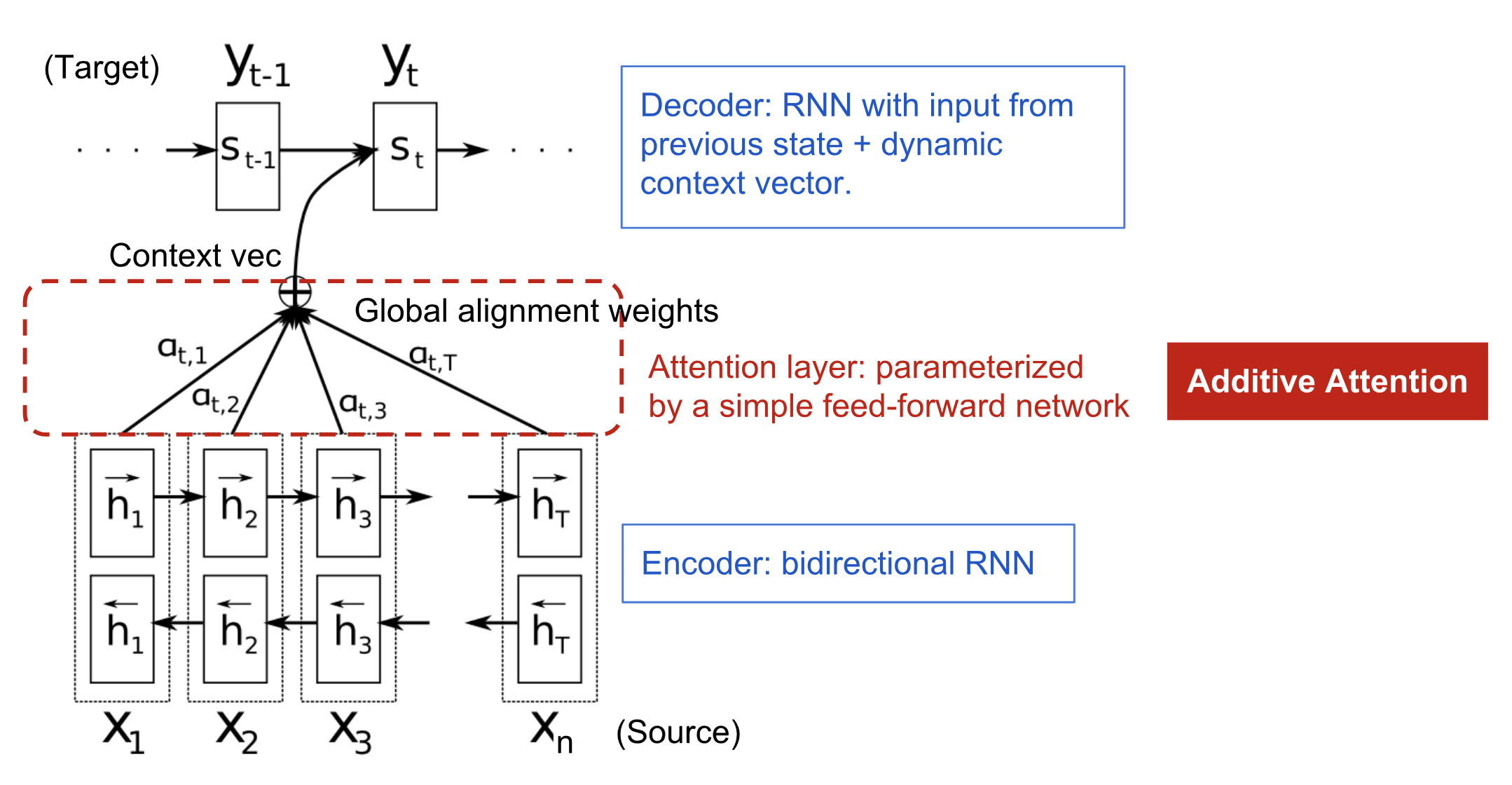
注意力机制的诞生是为了帮助神经机器翻译（NMT）记忆长句。注意力发明的秘诀是在上下文向量和整个源输入之间创建捷径，而不是从编码器的最后一个隐藏状态中建立一个单一的上下文向量。这些捷径连接的权重可针对每个输出元素进行定制。

虽然上下文向量可以访问整个输入序列，但我们不必担心遗忘问题。源代码和目标代码之间的对齐是由上下文向量学习和控制的。从本质上讲，上下文向量需要消耗三项信息：

编码器隐藏状态
解码器隐藏状态
源和目标之间的对齐

1.3. 一系列注意力机制

1.3.1. 概括

下面是几种流行的注意力机制和相应的对齐评分函数的汇总表：

名称	对齐评分函数	引用
Content-base attention	$score(s_t, h_i) = cosine[s_t, h_i]$	Graves2014
Additive(*)	$score(s_t, h_i) = v^T_atanh(W_a[s_{t-1};h_i]$	Bahdanau2015
Location-Base	$\alpha_{t,i} = softmax(W_as_t)$	Luong2015
General	$score(s_t, h_i) = s^T_tW_ah_i$	Luong2015
Dot-Product	$score(s_t, h_i) = s^T_th_i$	Luong2015
Scaled Dot-Product(^)	$score(s_t, h_i) = \frac{s^T_th_i}{\sqrt{n}}$	Xu2015

以下是更广泛类别的注意力机制的摘要：

名称	对齐评分函数	引用
Self-Attention(&)	关联同一输入序列的不同位置。理论上，自注意力可以采用上述任何评分函数，但只需将目标序列替换为相同的输入序列即可。	Cheng2016
Global/Soft	关注整个输入状态空间。	Xu2015
Local/Hard	关注输入状态空间部分；即输入图像的一个 patch。	Luong2015

1.3.2. 自注意力

自注意力，也称为内部注意力，是一种将单个序列的不同位置相关联的注意力机制，以便计算同一序列的表示。它已被证明在机器阅读、抽象概括或图像描述生成中非常有用。

在下面的例子中，自注意力机制使我们能够学习当前单词和句子前一部分之间的相关性。

1.3.3. 软注意力 vs 硬注意力

本文首先根据注意力是访问整个图像还是仅访问一个补丁，提出了“软”注意力和“硬”注意力之间的区别：

软注意力：学习对齐权重，并将其 "柔和 "地置于源图像中的所有 Patch 上；这与 Bahdanau et al., 2015 中的关注类型基本相同。
- 优点：模型平滑且可微分
- 缺点：当源输入很大时，成本昂贵
硬注意力：一次只选择要注意的图像的一个 patch
- 优点：推理时的计算量较少
- 缺点：该模型是不可微分的，需要更复杂的技术（例如方差减少或强化学习）来训练

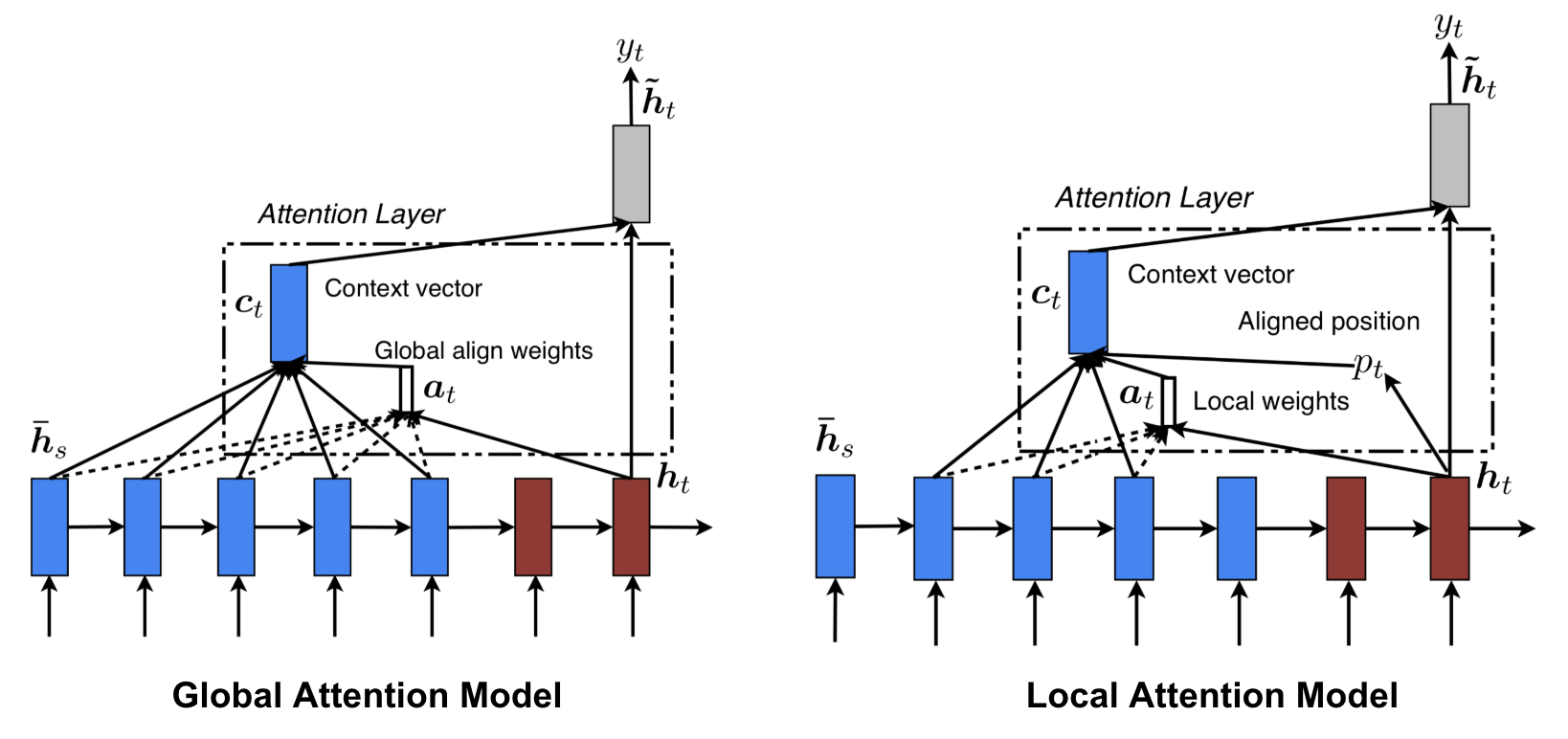
1.3.4. 全局注意力 vs 局部注意力

Luong, et al., 2015 提出了“全局”和“局部”注意力。全局注意力类似于软注意力，而局部注意力是硬注意力和软注意力的有趣混合，是对硬注意力的改进，使其可微分：模型首先预测当前目标词的单一对齐位置，然后使用以源位置为中心的窗口计算上下文向量。

1.4. Transformer

毫无疑问，“Attention is All you Need” 是 2017 年最具影响力和最有趣的论文之一。它对软注意力进行了大量改进，使得在没有递归网络单元的情况下进行 seq2seq 建模成为可能。所提出的 "transformer" 模型完全建立在自注意机制上，而不使用序列对齐的递归架构。

1.4.1. Key, Value and Query

Transformer 中的主要组件是多头自注意力机制单元。 Transformer 将输入的编码表示视为一组 key-value 对，(K, V)，维度均为 $n$ （输入序列长度）；在 NMT（Neural Machine Translation）的上下文中，键和值都是编码器隐藏状态。在解码器中，先前的输出被压缩为 query（维度为 $m$ 的 Q），并且通过映射此查询以及键和值集来生成下一个输出。

Transformer 采用缩放点积注意力：输出是 value 的加权和，其中分配给每个值的权重由 query 与所有 key 的点积确定：

$\text{Attention}(\mathbf{Q}, \mathbf{K}, \mathbf{V}) = \text{softmax}(\frac{\mathbf{Q}\mathbf{K}^\top}{\sqrt{n}})\mathbf{V}$

1.4.2. 多头注意力

多头机制不是只计算一次注意力，而是多次并行地运行缩放的点积注意力。独立的注意力输出被简单串联并线性转换为预期维度。我想这是因为集成总是有帮助的吧？根据论文所述，"多头注意允许模型联合注意来自不同位置的不同表征子空间的信息。如果只有一个注意力集中的头，平均值就会抑制这一点。"。

$\begin{aligned} \text{MultiHead}(\mathbf{Q}, \mathbf{K}, \mathbf{V}) &= [\text{head}_1; \dots; \text{head}_h]\mathbf{W}^O \\ \text{where head}_i &= \text{Attention}(\mathbf{Q}\mathbf{W}^Q_i, \mathbf{K}\mathbf{W}^K_i, \mathbf{V}\mathbf{W}^V_i) \end{aligned}$

1.4.3. 编码器

编码器生成基于注意力的表示，能够从潜在无限大的上下文中定位特定的信息。

N=6 个相同层的堆叠。
每层都有一个多头自注意力层和一个简单的位置全连接前馈网络
每个子层都采用残差连接和层归一化。所有子层输出相同维度 $d_{model} = 512$ 的数据。

1.4.4. 解码器

解码器能够从编码表示中检索。

N = 6 个相同层的堆叠
每层都有两个多头注意力机制子层和一个全连接前馈网络子层。[
与编码器类似，每个子层都采用残差连接和层归一化。
第一个多头注意子层被修改以防止位置关注后续位置，因为我们不希]()望在预测当前位置时关注未来的目标序列。

Lilian-Attention?Attention!